Test of standard theorem styles

Ahlfors' Lemma gives the principal criterion for obtaining lower bounds on the Kobayashi metric.

Ahlfors' Lemma 1 Let ds² = h(z) $\lvert$ dz $\rvert^{2}_{}$ be a Hermitian pseudo-metric on D_r, h∈C²(D_r), with ω the associated (1, 1)-form. If Ric $\nolimits$ ω≥ω on D_r, then ω≤ω_r on all of D_r (or equivalently, ds²≤ds_r²).

Lemma 1.1 (negatively curved families) Let {ds₁²,..., ds_k²} be a negatively curved family of metrics on D_r, with associated forms ω¹, ..., ω^k. Then ωⁱ≤ω_r for all i.

Then our main theorem:

Theorem 1.2 Let d_max and d_min be the maximum, resp. minimum distance between any two adjacent vertices of a quadrilateral Q. Let σ be the diagonal pigspan of a pig P with four legs. Then P is capable of standing on the corners of Q iff

σ≥ $\displaystyle \sqrt{{d_{\max}^2+d_{\min}^2}}$ .

(1)

Corollary 1.3 Admitting reflection and rotation, a three-legged pig P is capable of standing on the corners of a triangle T iff () holds.

Remark 1 As two-legged pigs generally fall over, the case of a polygon of order 2 is uninteresting.

Exercise 1 Generalize Theorem to three and four dimensions.

Note 1 This is a test of the custom theorem style `note'. It is supposed to have variant fonts and other differences.

B-Theorem 1
Test of the `linebreak' style of theorem heading.

This is a test of a citing theorem to cite a theorem from some other source.

1 (Theorem 3.6 in [1]) No hyperlinking available here yet ... but that's not a bad idea for the future.

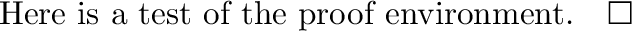
$\begin{proof} Here is a test of the proof environment. \end{proof}$

$\begin{proof} % latex2html id marker 113 [Proof of Theorem \ref{pigspan}] And another test. \end{proof}$

$\begin{proof}[Proof (necessity)] And another. \end{proof}$

$\begin{proof}[Proof (sufficiency)] And another. \end{proof}$